Apalache trail tips: how to check your specs faster
Difficulty: Red trail – Medium
This tutorial collects tips and tricks that demonstrate the strong sides of Apalache.
Tip 1: Use TLA+ constructs instead of explicit iteration
The Apalache
antipatterns mention that
one should not use explicit iteration (e.g., ApaFoldSet and
ApaFoldSeqLeft), unless it is really needed. In
this tip, we present a concrete example that demonstrates how explicit
iteration slows down Apalache.
In our example, we model a system of processes from a set Proc that are
equipped with individual clocks. These clocks may be completely unsynchronized.
However, they get updated uniformly, that is, all clocks have the same speed.
Let's have a look at the first part of this specification:
-------------------------- MODULE FoldExcept ----------------------------------
(*
* This specification measures performance in the presence of an anti-pattern.
*)
EXTENDS Integers, Apalache
CONSTANT
\* A fixed set of processes
\*
\* @type: Set(Str);
Proc
VARIABLES
\* Process clocks
\*
\* @type: Str -> Int;
clocks,
\* Drift between pairs of clocks
\*
\* @type: <<Str, Str>> -> Int;
drift
As we can see, the constant Proc is a specification parameter. For instance,
it can be equal to { "p1", "p2", "p3" }. The variable clocks assigns a
clock value to each process from Proc, whereas the variable drift collects
the clock difference for each pair of processes from Proc. This relation
is easy to see in the predicate Init:
Init ==
/\ clocks \in [ Proc -> Nat ]
/\ drift = [ <<p, q>> \in Proc \X Proc |-> clocks[p] - clocks[q] ]
Further, we write down a step of our system:
\* Uniformly advance the clocks and update the drifts.
\* Constructing functions without iteration.
NextFast ==
\E delta \in Nat \ { 0 }:
/\ clocks' = [ p \in Proc |-> clocks[p] + delta ]
/\ drift' = [ <<p, q>> \in Proc \X Proc |-> clocks'[p] - clocks'[q] ]
The transition predicate NextFast uniformly advances the clocks of all
processes by a non-negative number delta. Simultaneously, it updates the
clock differences in the function drift.
It is easy to see that drift actually does not change between the steps. We
can formulate this observation as an action
invariant:
\* Check that the clock drifts do not change
DriftInv ==
\A p, q \in Proc:
drift'[p, q] = drift[p, q]
Our version of NextFast is quite concise and it uses the good parts of
TLA+. However, new TLA+ users would probably write it differently. Below, you
can see the version that is more likely to be written by a specification
writer who has good experience in software engineering:
\* Uniformly advance the clocks and update the drifts.
\* Constructing functions via explicit iteration. More like a program.
NextSlow ==
\E delta \in Nat \ { 0 }:
/\ LET \* @type: (Str -> Int, Str) => (Str -> Int);
IncrementInLoop(clk, p) ==
[ clk EXCEPT ![p] = @ + delta ]
IN
clocks' = ApaFoldSet(IncrementInLoop, clocks, Proc)
/\ LET \* @type: (<<Str, Str>> -> Int, <<Str, Str>>)
\* => <<Str, Str>> -> Int;
SubtractInLoop(dft, pair) ==
LET p == pair[1]
q == pair[2]
IN
[ dft EXCEPT ![p, q] = clocks'[p] - clocks'[q] ]
IN
drift' = ApaFoldSet(SubtractInLoop, drift, Proc \X Proc)
The version NextSlow is less concise than NextFast, but it is probably easier to
read for a software engineer. Indeed, we update the variable clocks via
a set fold, which implements an iteration over the set of processes. What makes
it easier to understand for a software engineer is a local update in the
operator IncrementInLoop. Likewise, the variable drift is iteratively
updated with the operator SubtractInLoop.
If ApaFoldSet looks unfamiliar to you, check the page on folding sets and
sequences.
Although NextSlow may look more familiar, it is significantly harder for
Apalache to check than NextFast. To see the difference, we measure
performance of Apalache for several sizes of Proc: 3, 5, 7, and 10. We do
this by running Apalache for the values of N equal to 3, 5, 7, 10. To this
end we define several model files called MC_FoldExcept${N}.tla for
N=3,5,7,10. For instance, MC_FoldExcept3.tla looks as follows:
--------------------- MODULE MC_FoldExcept3 ---------------------------------
Proc == { "p1", "p2", "p3" }
VARIABLES
\* Process clocks
\*
\* @type: Str -> Int;
clocks,
\* Drift between pairs of clocks
\*
\* @type: <<Str, Str>> -> Int;
drift
INSTANCE FoldExcept
==============================================================================
We run Apalache for different instances of N:
apalache-mc check --next=NextSlow --inv=DriftInv MC_FoldExcept${N}.tla
apalache-mc check --next=NextFast --inv=DriftInv MC_FoldExcept${N}.tla
The plot below shows the running times for the versions NextSlow and
NextFast:
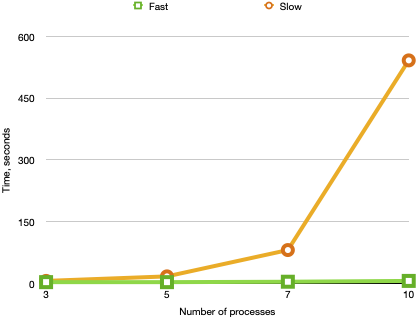
The plot speaks for itself. The version NextFast is dramatically faster than
NextSlow for an increasing number of processes. Interestingly, NextFast is
also more concise. In principle, both NextFast and NextSlow describe the
same behavior. However, NextFast looks higher-level: It looks like it
computes clocks and drifts in parallel, whereas NextSlow computes
these functions in a loop (though the order of iteration is unknown). Actually,
whether these functions are computed sequentially or in parallel is irrelevant
for our specification, as both NextFast and NextSlow describe a single
step of our system! We can view NextSlow as an implementation of NextFast,
as NextSlow contains a bit more computation details.
From the performance angle, the above plot may seem counterintuitive to
software engineers. Indeed, we are simply updating an array-like data structure
in a loop. Normally, it should not be computationally expensive. However,
behind the scenes, Apalache is producing constraints about all function
elements for each iteration. Intuitively, you can think of it as being fully
copied at every iteration, instead of one element being updated. From this
perspective, the iteration in NextSlow should clearly be less efficient.